FU 234 - Farbenumdeutung mit 2, 3 oder 4 Elementen
Musik und Mathematik – Gegensatz oder Vereinfachung?
Schnellzugriff
Musik und Mathematik
Dass es in der Musik mathematische Strukturen gibt, ist nichts Neues. Leider prallen bei der Vorstellung von einem künstlerischen Schaffen und dem Zusammentreffen mit der Mathematik scheinbare Welten aufeinander. Beim Umfang und der Komplexität der Musiktheorie ist der Musiker geneigt, sich nicht auch noch mit der hohen Kunst der Zahlenlehre zu beschäftigen. Aber gerade hier, wenn es auf den ersten Blick auch nicht so scheint, ist die Idee und die Umsetzung dieses Themenbereiches Minimalismus in Reinkultur. Der ganze Bereich der Strukturen basiert im Wesentlichen auf der Idee der Farbenumdeutung mit 2, 3 oder 4 Elementen (FU 234). Diese Konzeption wird auf die anderen Bereiche der Rhythmik, Motorik und der Variation von Elementen angewendet.
Ein Grundgedanke davon ist, eben NICHT rechnen zu müssen. Es ist eine leicht überschaubare Anwendung während des Musik Machens. Dies stellt im Gegensatz zu der bisherigen Krücke der Musiktheorie eine extreme Vereinfachung dar.
Farbenumdeutung
Für den etwas sperrigen Begriff: Farbenumdeutung mit 2, 3 oder 4 Elementen verwende ich im weiteren Verlauf die Kurzform FU234.
Sehr einfache mathematische Ideen werden mit Farben oder Formen durch serielle Anordnung, auf Positionen, abstrahiert. Diese dienen dann als Platzhalter für musikalische Elemente. Durch unterschiedliche Anordnung der Farben ergibt sich immer eine bestimmte Anzahl der möglichen Variationen. Dies hängt davon ab wie viele Elemente und wie oft diese verwendet werden.
Die Anzahl der verwendeten Farben und damit auch der Elemente und ebenso der Positionen ist von zwei bis auf maximal vier beschränkt. Dies hat den Hintergrund, dass die sich ergebenden Muster so klein und überschaubar bleiben, so dass sie auch während Improvisationen eingesetzt werden können. Die entstehenden Variationen und damit Gebrauchsmuster bezeichne ich kurz als Algo (Algorithmus).
Sie werden mit folgender Kurzschreibweise definiert:
X (Anzahl der Elemente) E (Elemente) X (Anzahl der Positionen) P (Positionen)
Welche Arten von Algos verwendet man?
Es gibt vier unterschiedliche Arten:
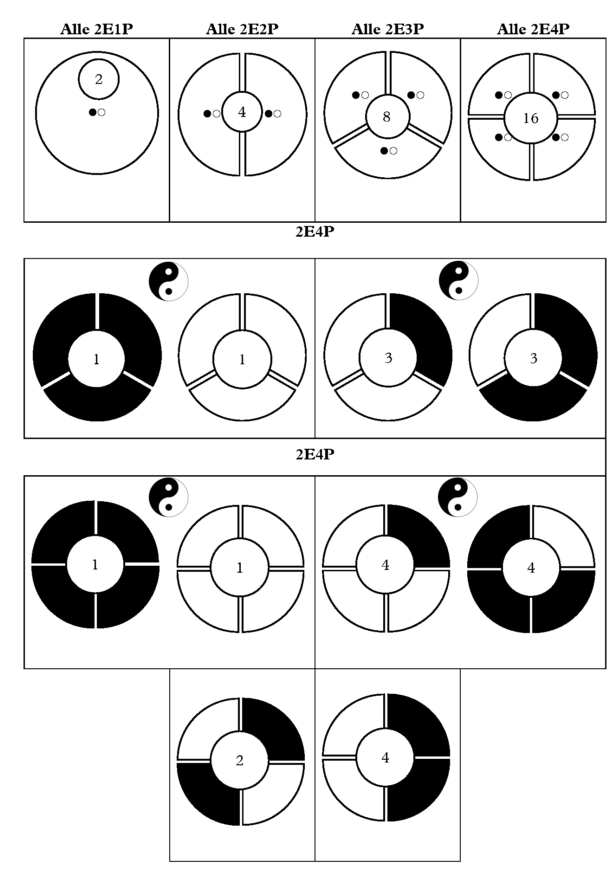
Binäre Algos – „Booleshit“ – 2ExP
Es werden nur zwei Elemente verwendet. Abgeleitet wird diese Vorgehensweise von der Booleschen Algebra, welche immer 2 Wahrheitswerte annimmt. Dies ist das logische Fundament für die digitale Computertechnologie, in der alle Rechenvorgänge mit an (1=wahr) oder aus (0=falsch) technisch umgesetzt werden. Um die Sache an dieser Stelle in eine Relation zu setzen, stellen wir uns die Terrabyte von Festplatten und Gigabyte von Arbeitsspeichern vor. Die Algos die ich an dieser Stelle für die Musik verwende haben lediglich 4 Bit und selbst diese werden mit ein paar Tricks auf 2 bis 3 Bit zusammengedampft. Es ist also nicht der Weg des theoretischen Gigantismus, sondern eher ein Weg des Minimalismus in Reinkultur. Der Einsatz von diesen zwei Elementen wird also auf die verwendeten Positionen genau wie beim binären Zahlensystem immer in Hochzahlen zur Basis 2 berechnet.
Hört sich komplizierter an als es ist:
Die Algos haben immer eine 2 bei den Elementen und als Farben verwende ich schwarz und weiß.
Die Algos wären:
- 2E1P – 2^1 = 2 Variationen
- 2E2P – 2^2 = 4 Variationen
- 2E3P – 2^3 = 8 Variationen
- 2E4P – 2^4 = 16 Variationen
- (2E5P – 2^5 = 32 Variationen)
- (2E6P – 2^6 = 64 Variationen)
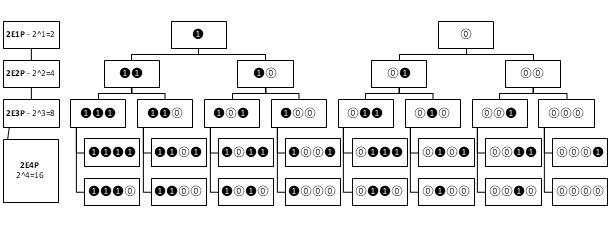
Wie man erkennen kann, sind die Algos mit 5 oder 6 Positionen schon eingeklammert, da die Anzahl der möglichen Variationen für die musikalische Praxis zu groß ist. Natürlich ist Musik so komplex, dass wir uns niemals nur auf 16 Variationen unserer Töne oder Rhythmen beschränken würden. Der Blickwinkel der FU234 legt aber den Fokus auf das Kleinste und man erhält durch mehrfache Kombination und Überlagerung der Algos schier unendliche Möglichkeiten.
Komplexere Strukturen erhalte ich durch Verbinden einfacherer Algos. Also z.B.: Nicht 2E8P (2^8=256), sondern zwei 2E4P (2^4=16) miteinander 16E2P (16^2=256) kombiniert. Das ergibt dann gleich viele Möglichkeiten, aber ich sehe immer meine 16 überschaubaren Variationen.
Kurzschreibweise Booleshit
Damit man auch eine zusammengefasste, bildhafte Vorstellung von dem Algo erhält, stelle ich diese in Kreisform dar. Dies ermöglicht alle Variationen auf dem Bild geistig nachzuvollziehen.
Die binären Algos stellen die Basis für alle binären und ternären Rhythmusfiguren dar. Sie können aber auch für viele andere Elemente als Platzhalter dienen.

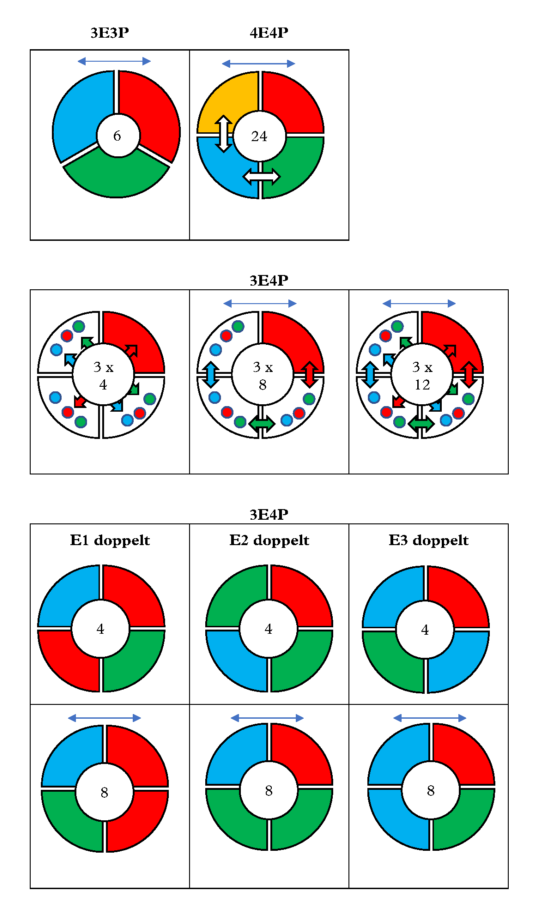
3 oder 4 Elemente auf eben so viel Positionen
Jedes Element kommt nur einmal vor. Wie bei einem Wettrennen, bei dem die Reihenfolge des Zieldurchlaufes die Position auf den Siegertreppen festlegt und nur einmal vergeben wird. Die Anzahl der Möglichkeiten ist dann immer die Fakultät der Positionen.
- 3E3P – 3! = 6 (3x2x1)
- 4E4P – 4! = 24 (4x3x2x1)
- (5E5P – 5! = 120)
Auch hier wird wieder deutlich, dass die rechnerische Anzahl von mehr als 4 Elementen den Rahmen der Übersichtlichkeit und damit der Anwendbarkeit sprengt.
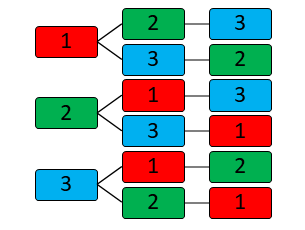
3 Elemente auf 3 Positionen – 3E3P
Jedes Element beginnt auf Position 1. Dann wird entschieden, wie es weiter geht. Dasselbe geschieht auf Position 2. Bei vier Positionen gibt es für die letzten beiden Positionen nur noch zwei Varianten. Es ergibt sich so ein „Entscheidungsbaum“. Gerade im musikalischen Kontext ist diese Form sehr praktikabel, da die Variationsmöglichkeit durch die Festlegung des ersten Elementes schon vorgegeben ist und kurze Wege zur Entscheidungsfindung führen.
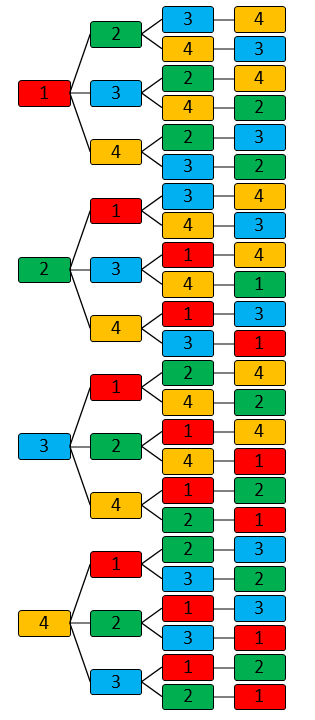
4 Elemente auf 4 Positionen – 4E4P
Es ergeben sich bei diesem Algo 4 x 3 x 2 x 1 = 24 Variationsmöglichkeiten. Mathematisch ausgedrückt auch Fakultät von 4 (geschrieben: 4!)
3 Elemente auf 4 Positionen doppeltes Element – 3E4P
Wenn wir 3 Elemente auf 4 Positionen haben, ergibt sich automatisch, dass eines doppelt vorkommt. Dies ist einerseits eine Vereinfachung, da sich bei der Verdoppelung die Anzahl der Möglichkeiten von 24 auf 12 halbiert. Formel dafür wäre 4! / 2! = 12. Allerdings könnte das erste, das zweite oder auch das dritte doppelt auftauchen. Deshalb ergibt es sich, dass sich drei unterschiedliche Algos ergeben, welche allerdings nach denselben Mustern aufgebaut sind. Außerdem kann es sein, dass das doppelte Element benachbart ist oder es von den anderen beiden umrahmt wird. Dies wird wiederum gesondert betrachtet. Wenn der gesamte Vorgang betrachtet wird, ergeben sich insgesamt 36 Variationsmöglichkeiten. Diese können aber in 3 x (4 + 8) = 36 zerlegt werden.
- 3E4P = 3 x (4 + 8) = 36 Variationen
3 Elemente auf 4 Positionen – 3E4P
Das erste Element ist mit Abstand doppelt
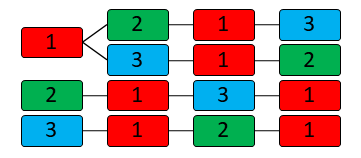
Das erste Element ist benachbart doppelt
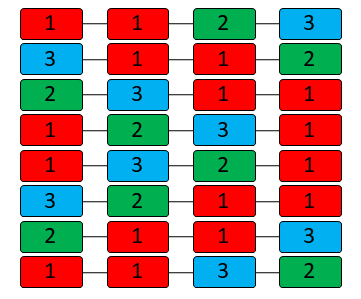
Kurzschreibweise FU 234

Zusammenfassung
- Algos der Farbenumdeutung haben 2-4 Elemente auf 2-4 Positionen
- Kurzschreibweise der Algos:
X (Anzahl der Elemente) E (Elemente) X (Anzahl der Positionen) P (Positionen) -xExP - Es gibt 3 Arten von Algos
1. binäre (s/w)
2. Gleich viel Elemente wie Positionen
3. Doppelte Elemente - 2E2P= 4 Variationen
2E3P = 8 Variationen
2E4P = 16 Variationen - 3E3P = 6 Variationen
4E4P = 24 Variationen - 3E4P = 3 x (4 + 8) = 3 x 12 = 36 Variationen
- Binäre Algos sind die Grundlage für alle Rhythmusfiguren